一、sparse模块：

python中scipy模块中，有一个模块叫sparse模块，就是专门为了解决稀疏矩阵而生。本文的大部分内容，其实就是基于sparse模块而来的

导入模块：from scipy import sparse

二、七种矩阵类型

1. coo_matrix
2. dok_matrix
3. lil_matrix
4. dia_matrix
5. csr_matrix
6. csc_matrix
7. bsr_matrix

三、coo_matrix

coo_matrix是最简单的存储方式。采用三个数组row、col和data保存非零元素的信息。这三个数组的长度相同，row保存元素的行，col保存元素的列，data保存元素的值。一般来说，coo_matrix主要用来创建矩阵，因为coo_matrix无法对矩阵的元素进行增删改等操作，一旦矩阵创建成功以后，会转化为其他形式的矩阵。data = [5,2,3,0]

>>> row = [2,2,3,2]>>> col = [3,4,2,3]>>> c = sparse.coo_matrix((data,(row,col)),shape=(5,6))>>> print c.toarray()[[0 0 0 0 0 0] [0 0 0 0 0 0] [0 0 0 5 2 0] [0 0 3 0 0 0] [0 0 0 0 0 0]]

稍微需要注意的一点是，用coo_matrix创建矩阵的时候，相同的行列坐标可以出现多次。矩阵被真正创建完成以后，相应的坐标值会加起来得到最终的结果。

四、dok_matrix与lil_matrix

dok_matrix和lil_matrix适用的场景是逐渐添加矩阵的元素。

doc_matrix的策略是采用字典来记录矩阵中不为0的元素。自然，字典的key存的是记录元素的位置信息的元祖，value是记录元素的具体值。

>>> import numpy as np>>> from scipy.sparse import dok_matrix>>> S = dok_matrix((5, 5), dtype=np.float32)>>> for i in range(5):...     for j in range(5):...             S[i, j] = i + j...>>> print S.toarray()[[ 0.  1.  2.  3.  4.] [ 1.  2.  3.  4.  5.] [ 2.  3.  4.  5.  6.] [ 3.  4.  5.  6.  7.] [ 4.  5.  6.  7.  8.]]

lil_matrix则是使用两个列表存储非0元素。data保存每行中的非零元素,rows保存非零元素所在的列。这种格式也很适合逐个添加元素，并且能快速获取行相关的数据。

>>> from scipy.sparse import lil_matrix>>> l = lil_matrix((6,5))>>> l[2,3] = 1>>> l[3,4] = 2>>> l[3,2] = 3>>> print l.toarray()[[ 0.  0.  0.  0.  0.] [ 0.  0.  0.  0.  0.] [ 0.  0.  0.  1.  0.] [ 0.  0.  3.  0.  2.] [ 0.  0.  0.  0.  0.] [ 0.  0.  0.  0.  0.]]>>> print l.data[[] [] [1.0] [3.0, 2.0] [] []]>>> print l.rows[[] [] [3] [2, 4] [] []]

五、dia_matrix

这是一种对角线的存储方式。其中，列代表对角线，行代表行。如果对角线上的元素全为0，则省略。

如果原始矩阵是个对角性很好的矩阵那压缩率会非常高。

找了网络上的一张图，大家就很容易能看明白其中的原理。

六、csr_matrix与csc_matrix

csr_matrix，全名为Compressed Sparse Row，是按行对矩阵进行压缩的。CSR需要三类数据：数值，列号，以及行偏移量。CSR是一种编码的方式，其中，数值与列号的含义，与coo里是一致的。行偏移表示某一行的第一个元素在values里面的起始偏移位置。

同样在网络上找了一张图，能比较好反映其中的原理。

以官方文档为例，此时data代表的是存储的值的数组，indices代表的是每一行中第几列有对应data中的元素，即从indices中可以推断出列的信息，

indptr则用来推断出行的信息，默认元素开始为0，第一个元素为2，则证明第一行中有2-0=2个元素，所以将data数组中前另个元素写入第一行中，而indices前两个元素为0,2，则代表第0列和第2列。前两第二个元素为3，证明第二行中有3-2=1个元素，该元素为data[2]=3,且存储在indices[2] = 2列中。依次类推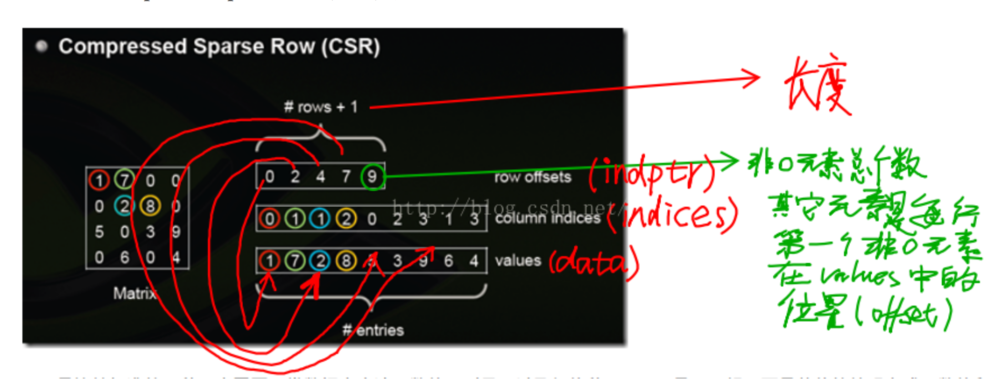

>>> from scipy.sparse import csr_matrix>>> indptr = np.array([0, 2, 3, 6])>>> indices = np.array([0, 2, 2, 0, 1, 2])>>> data = np.array([1, 2, 3, 4, 5, 6])>>> csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()array([[1, 0, 2],       [0, 0, 3],       [4, 5, 6]])

不难看出，csr_matrix比较适合用来做真正的矩阵运算。

至于csc_matrix，跟csr_matrix类似，只不过是基于列的方式压缩的，不再单独介绍。

七、bsr_matrix

按分块的思想对矩阵进行压缩。

 

摘自：https://blog.csdn.net/bitcarmanlee/article/details/52668477